Write a Java program that prints the length of the longest sorted (in ascending order) subarray of a given unsorted array of 10 integers.

-- Example: If input array is ==== 4 2 1 5 6 4 2 6 -1 5

then the output should be 3.

-- Ask the user to enter the 10 integers from the keyboard.

-- Print the last answer only (No other messages should be printed in the program)

-- VPL evaluation is not available in this exercise.

Suppose a certain population of observations is normally distributed. What percentage of the observations in the population

Are within ±1.5 standard deviations of the mean?

Are more than 2.5 standard deviations above the mean?

Are more than 3.5 standard deviations away from (above or below) the mean?

A) Imagine you want to conduct a qualitative study using semi-structured interviews to explore 10 MBA graduates’ perceptions and experiences of searching for the first job after graduating from a private university in Karachi, Pakistan.

Develop an Interview Guide comprising 7 - 10 questions to be used in the study. Remember the Interview Guide must be developed by you, and not copied from any other source.

B) Suppose you have conducted 10 interviews using the interview guide you developed for part A of this question. List down at least 10 steps that you will take to conduct the thematic analysis of the interview data.

1. Quality and Appropriateness of Interview Questions
2. Coverage of the key aspects of the research topic
3. Appropriate steps for conducting thematic analysis:

Assume that you are a new analyst hired to evaluate the capital budgeting projects of the company which is considering investing in two CPEC projects, “Expansion Zone North” and “Expansion Zone East”. The initial cost of each project is Rs. 10,000. Company discount all projects based on WACC. Further, all the projects are equally risky projects and the company uses only debt and common equity for financing these projects. It can borrow unlimited amounts at an interest rate of rd 10% as long as it finances at its target capital structure, which calls for 50% debt and 50% common equity. The dividend for next period is $2.0, its expected that they will grow at the constant growth rate of 8%, and the company’s common stock sells for $20. The tax rate is 50%.

The cash flows of both the projects are given in table below:

Time Expansion Zone North
Cashflows (amount in Rs.) Expansion Zone East
Cashflows (amount in Rs.)
0 - 10,000 - 10,000
1 6,500 3,500
2 3,000 3,500
3 3,000 3,500
4 1,000 3,500

Carefully analyze the above table and answer the following questions in detail.
I. Calculate the weighted average cost of capital for this firm? (2.5 marks)
II. Compute each project’s IRR, NPV, payback, MIRR, and discounted payback. (2.5 Marks)
III. Which project(s) should be accepted if they are mutually exclusive? Explain (1.5 Marks)
IV. Which project(s) should be accepted if they are independent? Explain (1.5 Marks)

Assume hedger takes hedge ratio as h*, i.e, if the risk exposure is a long position of 100 units of spot commodity, to hedge the risk, hedger will short 100h* futures underlying on that commodity.

c) To make the hedge portfolio risk-free, the value of the portfolio should not vary no matter stock price rises or falls (or, equivalently, the hedge portfolio should not make profit in one state and make loss in the other, where the state means stock price rises or falls). Please based on the above fact, solve the optimal hedge ratio h*.

d) To make the hedge portfolio risk-free, the hedge portfolio should not make profit in one state and make loss in the other, where the state means stock price rises or falls. Please use the optimal hedge ratio solved in (c) to verify this fact.

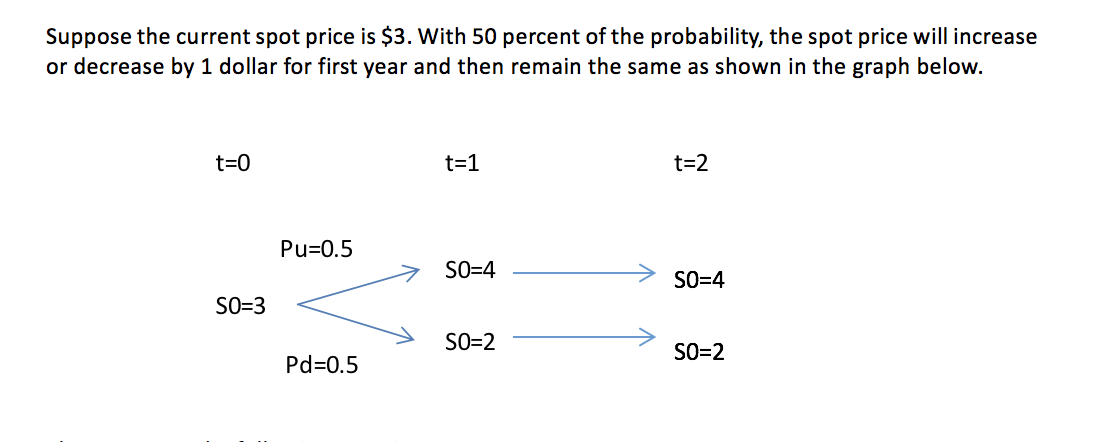
Suppose the current spot price is $3. With 50 percent of the probability, the spot price will increase or decrease by 1 dollar for first year and then remain the same as shown in the graph below.

A 13-year-old girl collapsed on a playground at school. When her mother was contacted, she mentioned that her daughter had been losing weight and complaining of abdominal pain. The emergency squad noticed a fruity breath. What are the tests you would suggest to run and why?

b,a,d,c.

a=b,d,c.

c,d,a,b.

a,b,c,d.

d,a=b,c,